320x100
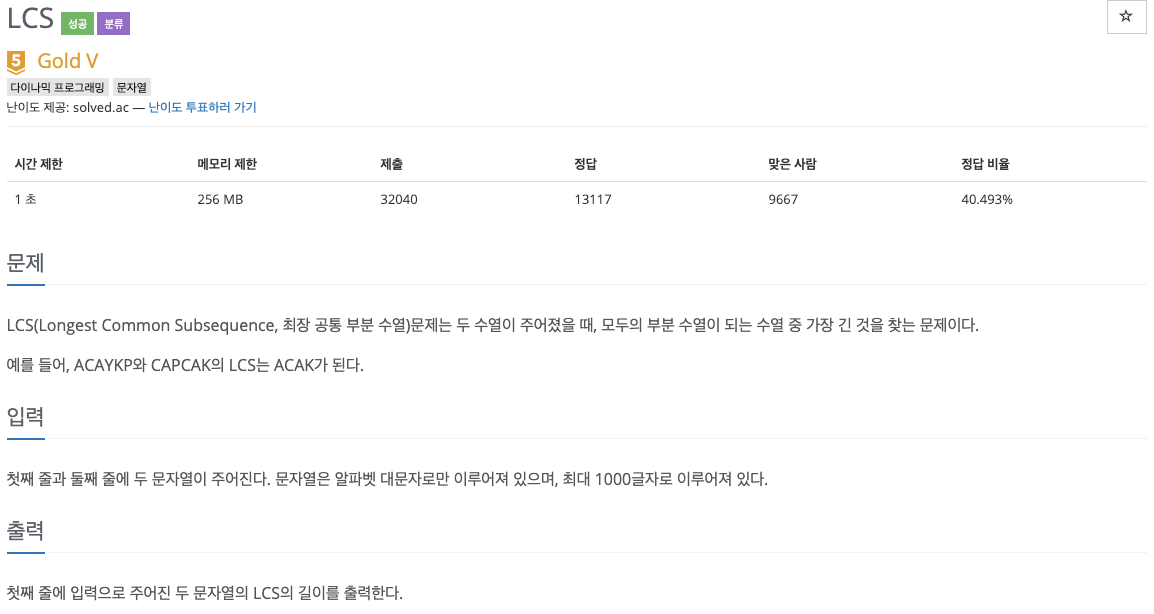
9251번 : LCS
다른 방법이 딱히 떠오르지 않는다면 DP로 접근하는게 좋은 것 같다.
이 문제를 풀 때 두 단계가 있다고 하면, 먼저 이 문제가 DP로 풀린다는 것을 알기 전과 후로 나눌 수 있을 것 같다.
이전에도 이와 비슷한 문제를 푼 적이 있었는데, 그때는 연속된 수열만 취급하는 문제였기 때문에 좀더 풀기 쉬웠다.
그러나 이 문제는 연속되지 않아도(서로 떨어져 있어도) 취급하기 때문에 조금 더 어렵다.
내 코드:
# dawitblog.tistory.com
# 입력
s1 = input()
s2 = input()
l1 = len(s1)
l2 = len(s2)
# dp 테이블
dp = [[0]*(l2+1) for _ in range(l1+1)]
for i in range(l1):
for j in range(l2):
if s1[i] == s2[j]:
dp[i+1][j+1] = dp[i][j] + 1
else:
dp[i+1][j+1] = max(dp[i][j+1],dp[i+1][j])
# 출력
print(dp[-1][-1])
dp[i][j]는 s1의 i+1 번째, s2의 j+1 번째까지의 문자열 중 LCS의 길이를 뜻한다. (예를 들어 dp[2][3] -> ACA와 CAPC의 최장 공통 수열의 길이)
이중 for 문을 돌면서 문자를 하나씩 추가한다. 이때 추가한 문자가 추가하지 않은 문자열의 마지막 문자와 같다면 해당 dp테이블의 값을 대각선 왼쪽 위의 값에서 1을 더한 값으로 지정한다.
만약 같지 않다면 해당 dp테이블을 값을 상단, 좌측 값중 작지 않은 값으로 정한다. LCS의 길이가 변하지 않기 때문이다.
'PS > solved.ac' 카테고리의 다른 글
| [CLASS 4]백준 12851번 - 숨바꼭질 2 (0) | 2021.03.25 |
|---|---|
| [CLASS 4]백준 9663번 - N-Queen (0) | 2021.03.23 |
| [CLASS 4]백준 1916번 - 최소비용 구하기 (0) | 2021.03.21 |
| [CLASS 4]백준 1753번 - 최단경로 (0) | 2021.03.16 |
| [CLASS 4]백준 16953번 - A → B (0) | 2021.03.15 |




댓글