320x100
1865번 - 웜홀
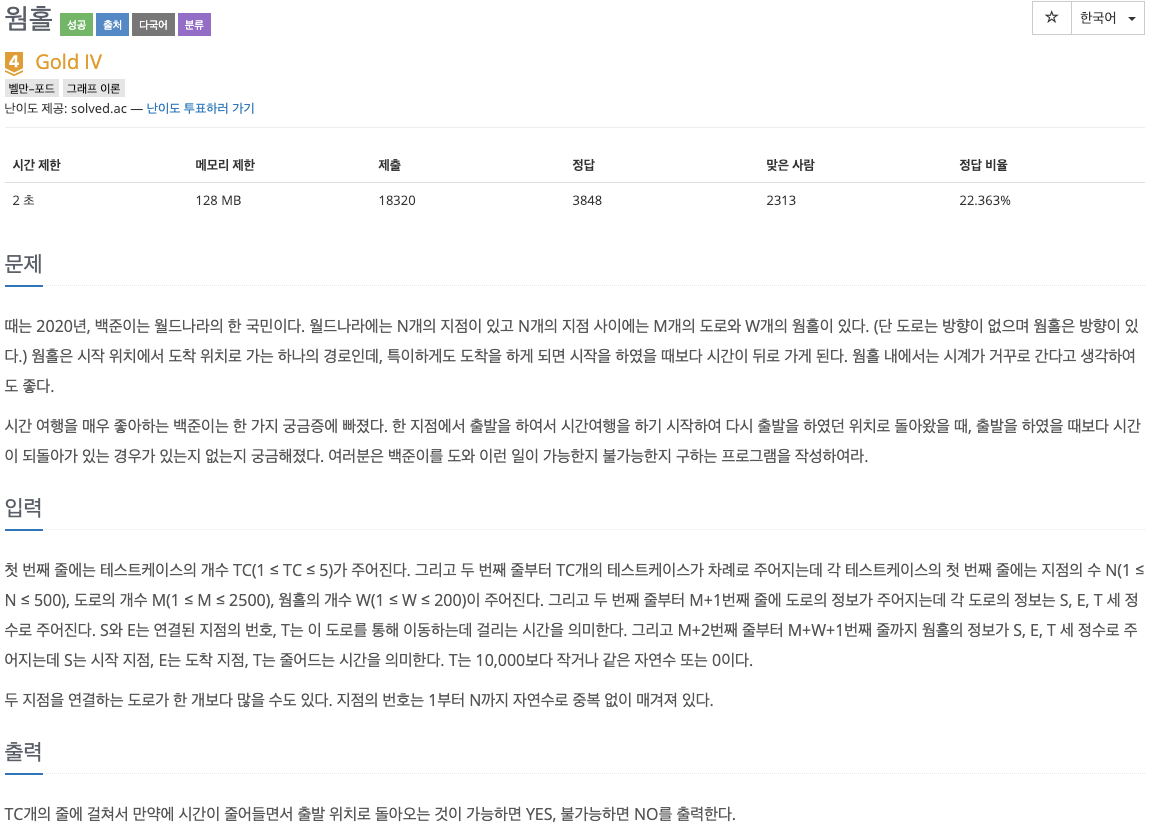
벨만-포드 알고리즘을 처음 접해본 나에게는 힘든 문제였다. 음의 간선이 존재하는 문제 자체가 처음이었기에 많이 고민하다가 플로이드-와샬 알로리즘으로도 시도해보려 했으나 모종의 이유(?)로 실패하고 벨만-포드 알고리즘을 적용하여 풀었다.
내 코드:
from sys import stdin
input = stdin.readline
INF = int(1e9)
def bf():
for i in range(1,n+1):
for now in range(1,n+1):
for dest, cost in nodes[now]:
if dist[dest] > dist[now] + cost:
dist[dest] = dist[now] + cost
if i == n:
return True
return False
T = int(input())
for _ in range(T):
n,m,w = map(int,input().split())
nodes = [[] for _ in range(n+1)]
dist = [INF] * (n+1)
for _ in range(m):
a,b,t = map(int,input().split())
nodes[a].append((b,t))
nodes[b].append((a,t))
for _ in range(w):
a,b,t = map(int,input().split())
nodes[a].append((b,-t))
print('YES' if bf() else 'NO')
보통의 밸만-포드 알고리즘은 모든 간선까지의 최단경로를 구하는 알고리즘이다. 그런데 이 문제는 시작점이 정해져 있지 않기 때문에, 만약 음의 사이클이 존재하기만 한다면 무조건 최소 2개 이상의 점에서 시작 시간보다 빠르게 도착하는것이 가능하다.
따라서 음의 사이클이 존재하는지만 찾으면 되고, 시작점을 설정할 필요가 없다.
음의 간선이 존재하는 문제를 처음 풀어봐서 생각하고 배우고 푸는데 시간이 많이 걸렸다. 이후에 음의 간선이 포함된 문제를 많이 풀어서 익숙해질 필요가 있다.
'PS > solved.ac' 카테고리의 다른 글
| [CLASS 4]백준 1967번 - 트리의 지름 (0) | 2021.05.08 |
|---|---|
| [CLASS 4]백준 1918번 - 후위 표기식 (0) | 2021.05.06 |
| [CLASS 4]백준 1504번 - 특정한 최단 경로 (0) | 2021.05.04 |
| [CLASS 4]백준 1043번 - 거짓말 (0) | 2021.05.01 |
| [CLASS 4]백준 17144번 - 미세먼지 안녕! (0) | 2021.04.29 |




댓글