[자료구조]우선순위 큐(Priority Queue)

정의

In computer science, a priority queue is an abstract data type similar to a regular queue or stack data structure in which each element additionally has a "priority" associated with it. In a priority queue, an element with high priority is served before an element with low priority. In some implementations, if two elements have the same priority, they are served according to the order in which they were enqueued, while in other implementations, ordering of elements with the same priority is undefined.

-Wikipedia

 

먼저 Queue라고 한다면, 먼저 들어간 데이터가 먼저 나오는, First in-First Out(FIFO) 구조를 가진 자료구조를 말한다. 그런데 여기에 Priority(우선순위)가 붙었다. 이는 일반적인 큐와 다르게 순서를 무시하고 각 key들의 우선순위가 높은 것부터 먼저 나온다는 것을 의미한다. 만약 두 원소가 같은 우선순위를 가지고 있다면, 큐에서와 같이 그 두 원소에 순서에 따라 처리된다.

 

널리 알려진 오류

우선순위 큐는 힙(heap)으로 많이 구현한다. 이때문에 우선순위 큐가 heap그 자체이다, 혹은 heap으로만 구현할 수 있다 라는 오해가 있다. 그러나 heap은 우선순위 큐를 구현하기 위한 하나의 방법일 뿐이다. 우선순위 큐는 heap 뿐만 아니라 배열이나, 연결 리스트 등의 다른 자료구조로도 구현될 수 있다. 다만, 배열이나 연결 리스트 등으로 잘 구현하지 않는 이유는, 시간 복잡도에 있다.

 

만약 우선순위 큐를 배열 혹은 연결 리스트로 구현한다고 해보자. 우선순위가 높은 것부터 순서대로 삽입한다고 가정하면, 우선순위가 가장 낮은 데이터가 들어왔을 경우에는 배열은 O(1)의 시간 복잡도를 가지지만, 연결 리스트는 삽입할 위치를 일일이 찾아야 하므로 O(n)의 시간 복잡도를 가진다. 또한 반대의 경우는 배열이 O(n)의 시간 복잡도를 가지게 된다.(물론 쉽게 구현할 수 있다는 장점도 있다)

 

heap의 경우는 완전 이진 트리의 구조로, 삽입 과정이든 삭제 과정이든 부모와 자식 간의 비교만 한다. 비교 시마다 남은 비교해야할 노드의 개수가 반씩 줄기 때문에 전체 노드의 개수를 n 이라고 할 때, 최선의 경우 O(1) 최악의 경우 O(log2n)의 시간 복잡도를 가지게 된다. 삽입과 삭제 과정의 시간 복잡도 편차가 크고 최악의 경우가 훨씬 느린 배열이나 연결 리스트로 구현하기보다는, heap으로 구현하는것이 훨씬 더 유리하기 때문에 heap으로 자주 구현하는 것이다. 이때문에 우선순위 큐는 heap으로만 구현할 수 있다는 오해가 생긴 것 같다.

 

주요 함수

삽입(insert,push)

우선순위 큐에서의 삽입은, 말 그대로 해당 자료구조에 값을 집어넣는 과정을 뜻한다. 다만 해당 우선순위 큐를 구현한 자료구조의 규칙에 따라 우선순위에 맞게 집어넣어야 한다.

 

 

예시는 최소 힙으로 구현한 우선순위 큐로 하겠다.

 

 

 

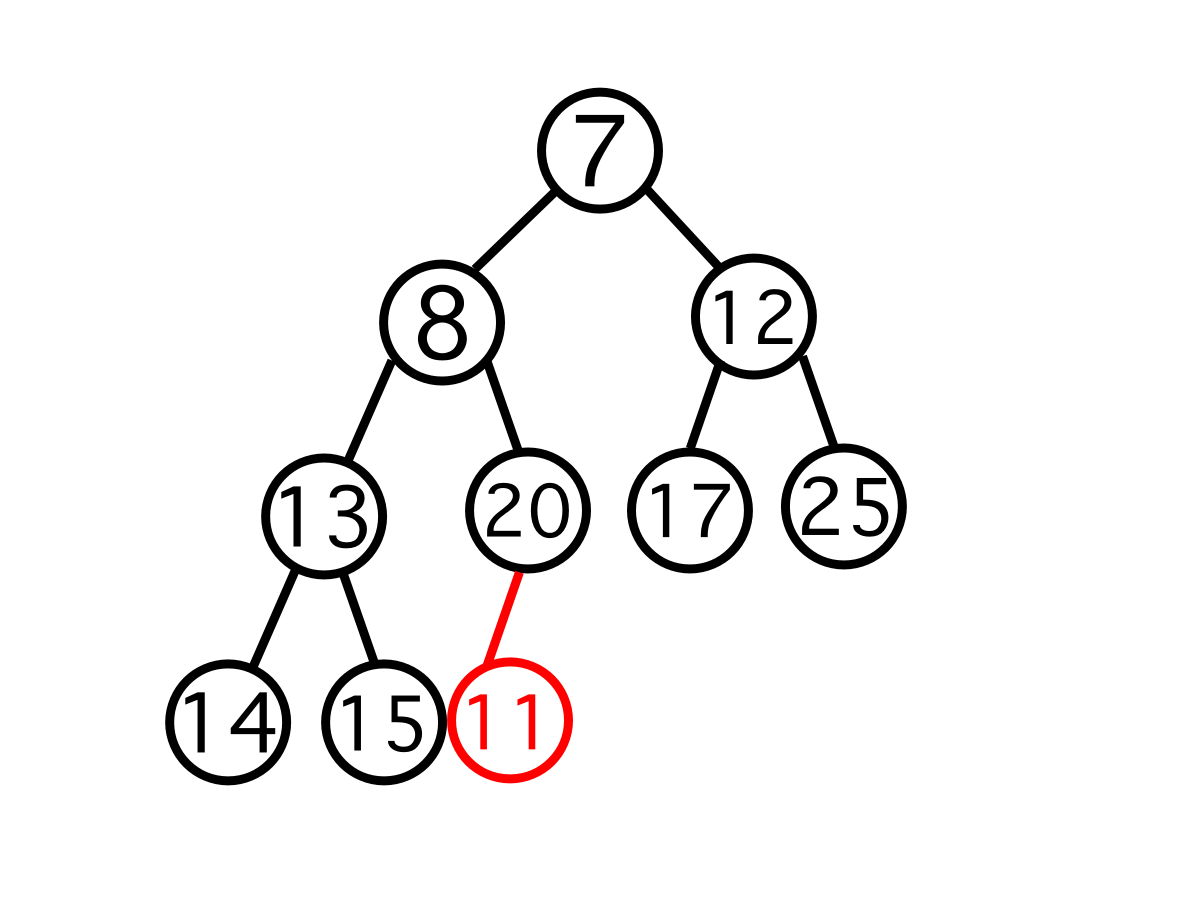
해당 최소 힙에서 11을 삽입한다고 할 때, 먼저 힙의 마지막 위치에 11을 삽입한다. '마지막 위치'란 삽입 후에도 완전 이진 트리를 유지할 수 있는 위치를 뜻한다

 

 

 

자신의 부모 노드와 자신 사이의 우선순위를 비교한다. 여기서는 11이 우선순위가 높으므로(값이 더 작으므로) 20과 자리를 교체한다.

 

 

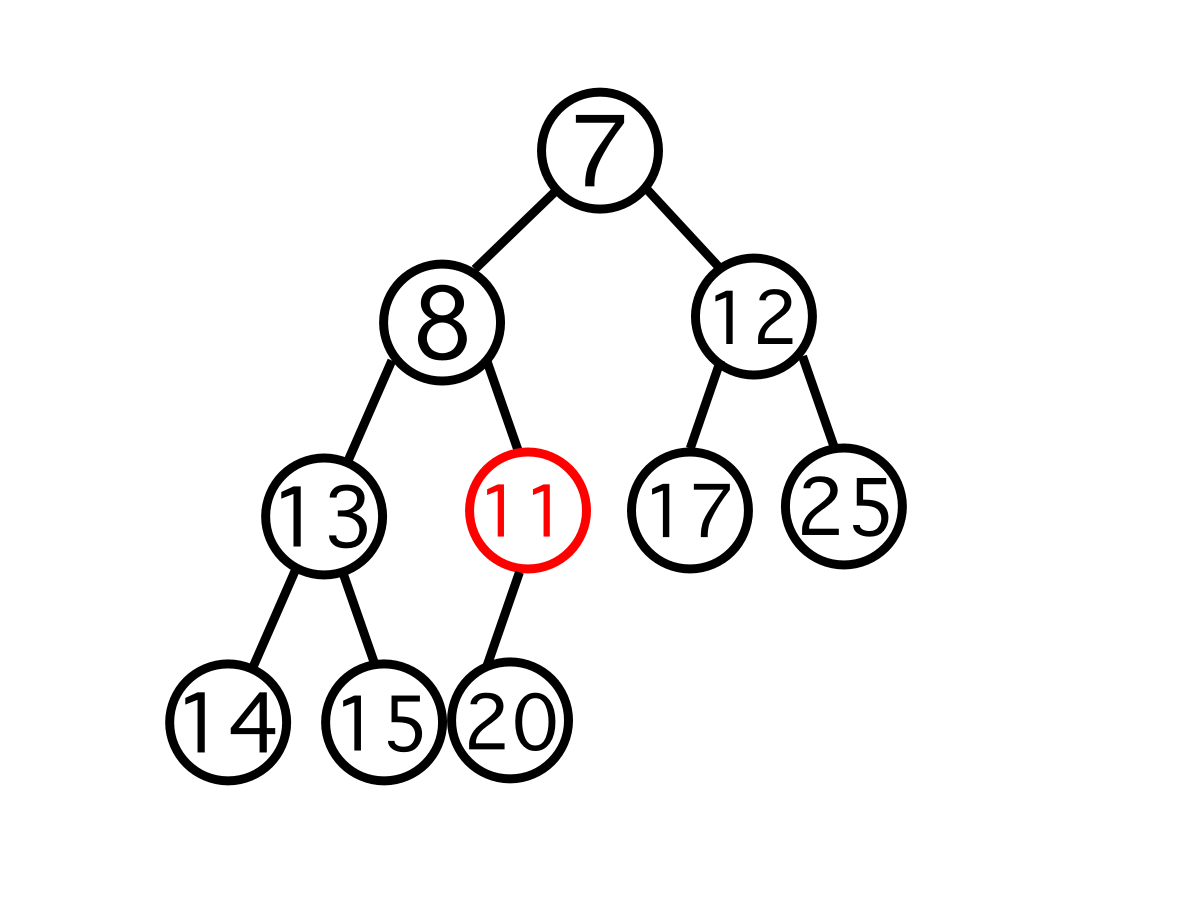
이 상태에서 이제 8과 비교했을 때 자기 자신보다 8이 우선순위가 높기 때문에 이 상태로 삽입 과정은 끝이 난다.

 

만약 최악의 경우로, 새로 추가한 노드의 위치가 높이가 늘어나는 위치라고 해도, 총 시간 복잡도 O(logn) 으로 삽입과정을 해결할 수 있다.

 

삭제(remove,pop)

삭제는 보통 우선순위 큐에서 우선순위가 가장 높은 값을 반환하고 삭제하는 과정을 뜻한다.

 

 

이 상태에서 값을 삭제한다면, 우선순위가 가장 높은 root의 값을 먼저 반환한 뒤

 

 

 

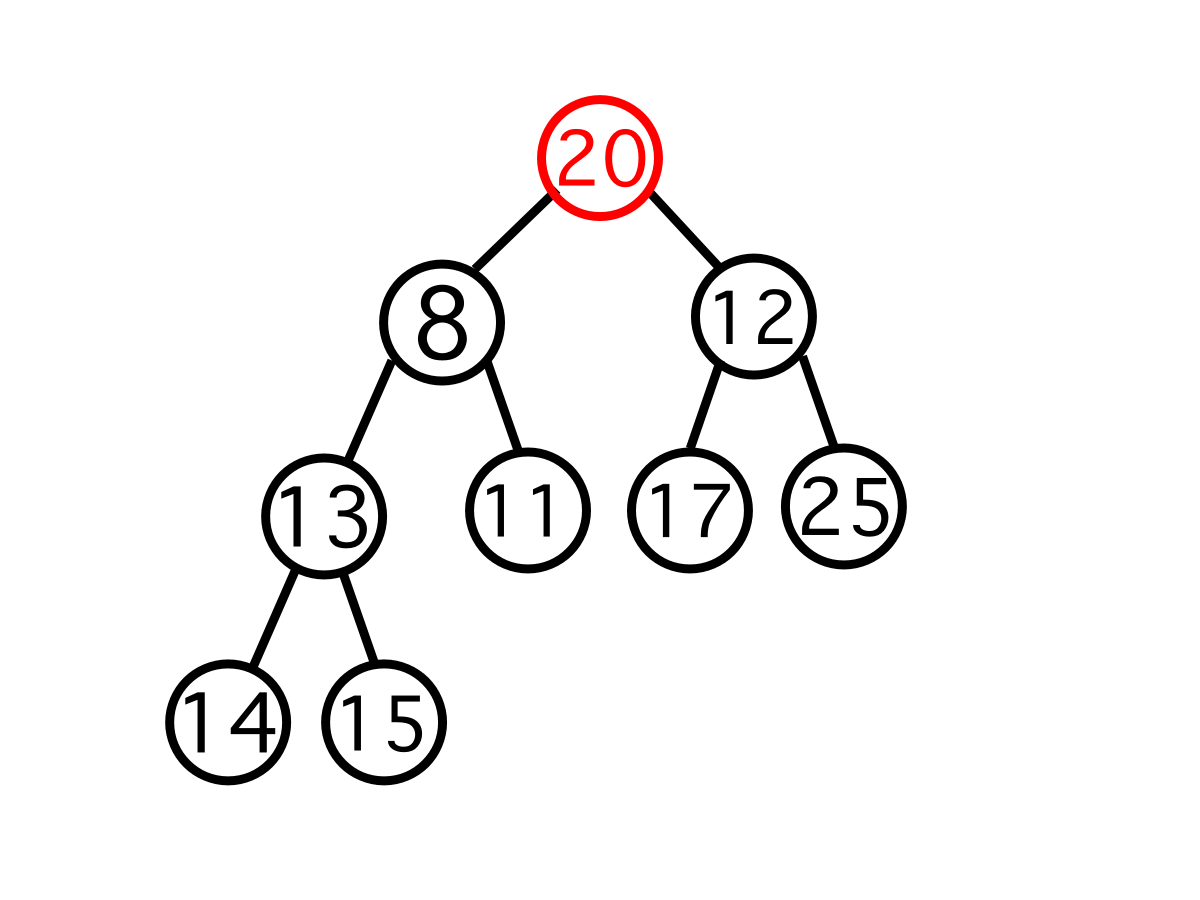
root를 삭제하고 '마지막 위치' 에 있던 값을 root로 일단 불러온다.

 

 

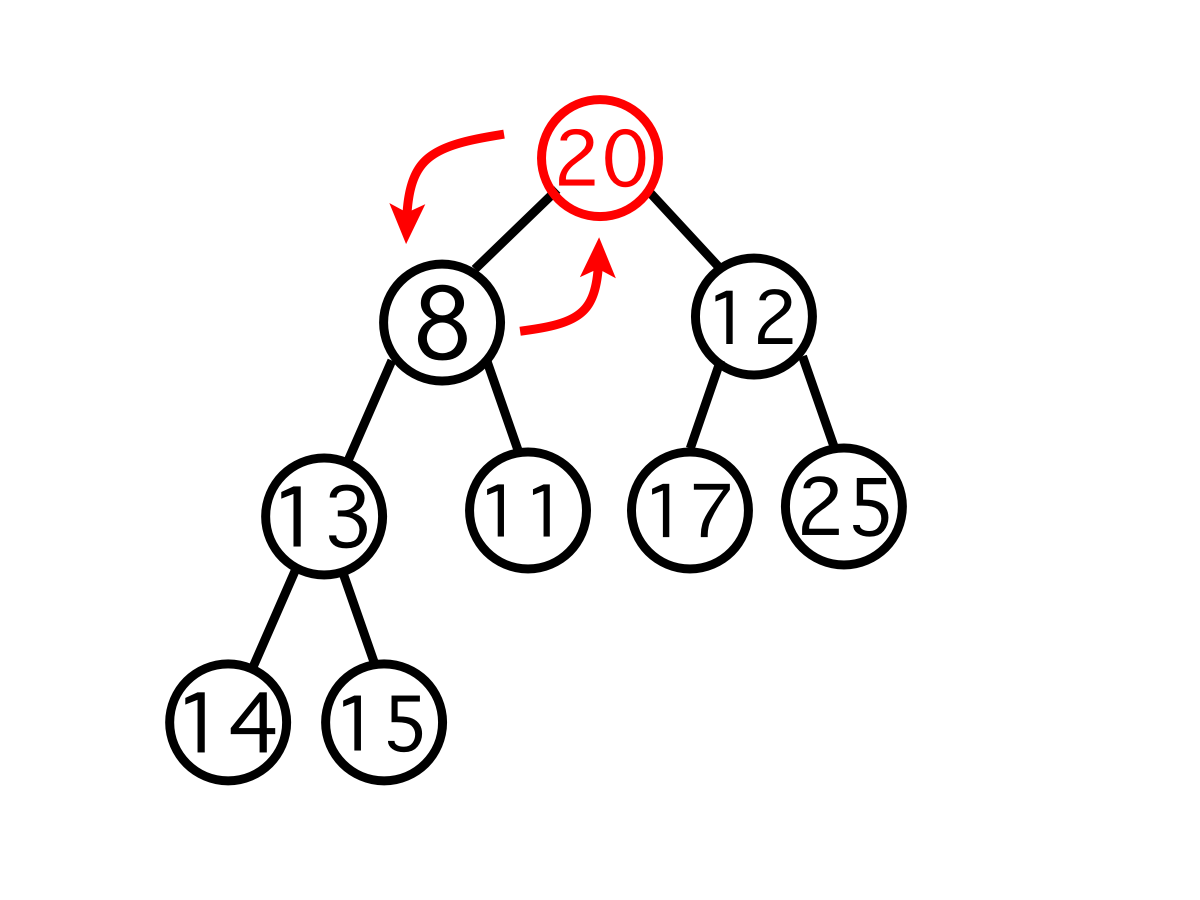
이제 자식 노드들과 우선순위를 비교하면 된다. 자식 노드가 자신보다 우선순위가 높다면 자리를 교체하면 된다.

이때 두 자식 노드 중 우선 순위가 높은(여기서는 수가 더 적은) 자식 노드와 자리를 교체해야 한다. 그래야 교체 후에 해당 노드가 비교 대상이었던 다른 노드보다 교체 후에 부모 노드가 된 뒤에도 우선 순위가 높다.

 

 

더이상 비교할 자식 노드가 없거나, 자식 노드들보다 우선순위가 크다면 삭제 과정은 비로소 끝난다. 삭제 과정 또한 루트로 올라왔던 노드가 가장 아래로 다시 내려가는 최악의 상황을 가정한다고 해도 시간 복잡도 O(logn)으로 해결할 수 있다.

 

구현

C++

#include <iostream>
using namespace std;

class PQ{
  int max_size;
  int size;
  int* q = nullptr;

public:
  PQ(int max_size){
    this->size = 0;
    this->max_size = max_size;
    q = new int[max_size+1];
  }

  bool insert(int value){
    if (size >= max_size){
      return false;
    }
    int ptr = ++size;
    q[ptr] = value;

    while (ptr/2>0 && q[ptr/2] > q[ptr]){
      swap(q[ptr],q[ptr/2]);
      ptr /= 2;
    }

    return true;
  }

  int pop(){
    if (size == 0){
      return -1;
    }

    int val = q[1];
    q[1] = q[size];
    size--;

    int parent = 1;
    int child = parent * 2;
    if (child + 1 <= size) {
      child = (q[child] < q[child + 1]) ? child : child + 1;
    }

    while (child <= size && q[parent] > q[child]) {
      swap(q[parent],q[child]);

      parent = child;
      child = child * 2;
      if (child + 1 <= size) {
        child = (q[child] < q[child + 1]) ? child : child + 1;
      }
    }

    return val;
  }

  int Size() { return size; }

  bool isEmpty() { return size == 0; }

  int top() { if (size == 0) return -1; else return q[1]; }

  void print() {
    if (size == 0){
      cout << -1 << endl;
      return;
    }
    for (int i = 1; i <= size; i++)
      cout << q[i] << " ";
    cout << endl;
  }
};