320x100
1238번 : 파티
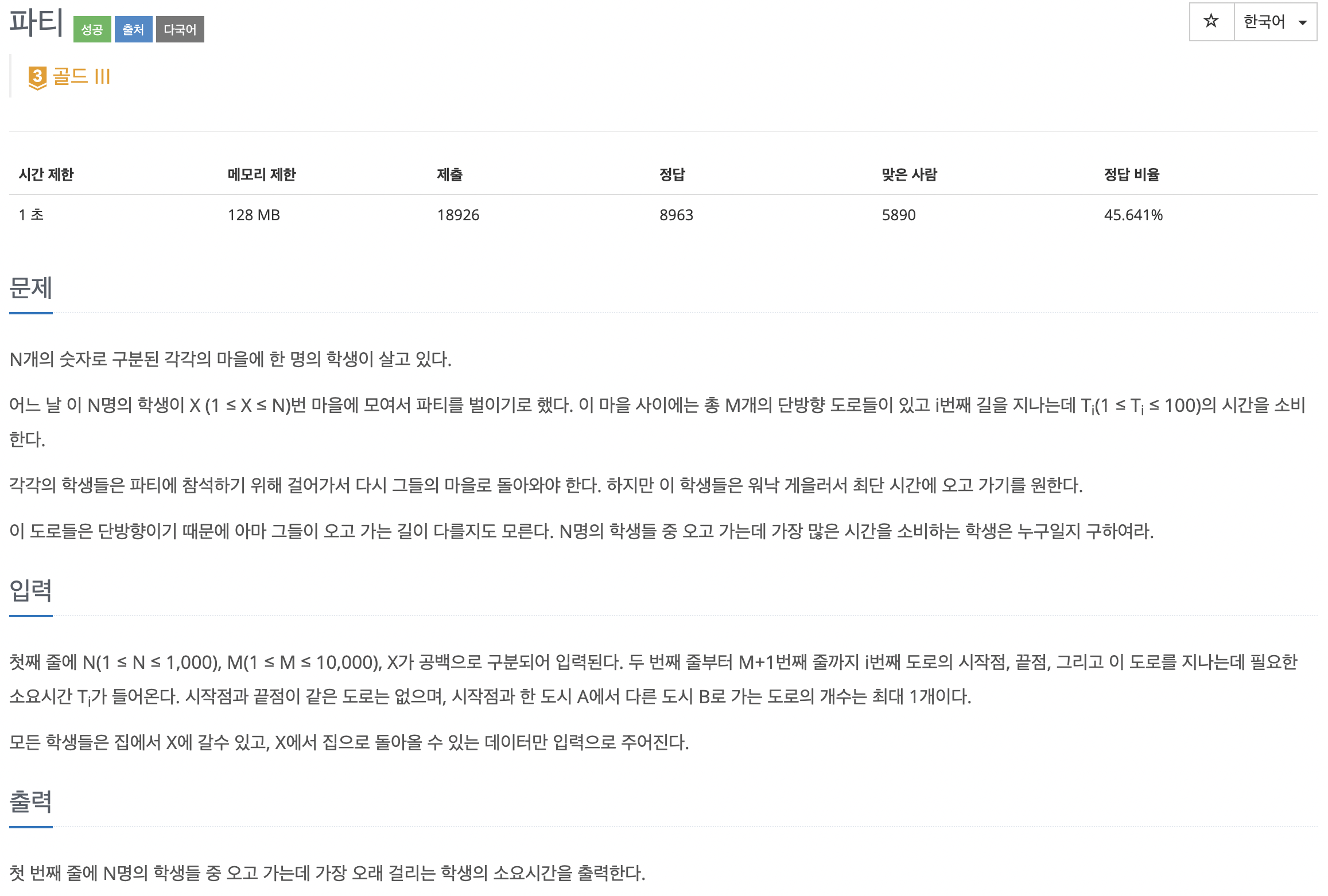
문제를 보고 가장 먼저 든 생각은 역시 코드를 작성하는 입장에서 가장 편한 플로이드 와샬 알고리즘이었다. 어렵지 않게 첫 시도를 해볼 수 있었다.
내 코드(플로이드 와샬, 시간 초과)
# dawitblog.tistory.com/169
import sys
input = sys.stdin.readline
INF = sys.maxsize
# 입력
n,m,x = map(int,input().split())
x -= 1
# 길 소요시간 리스트
roads = [[INF]*n for _ in range(n)]
for _ in range(m):
a,b,t = map(int,input().split())
a -= 1
b -= 1
roads[a][b] = t
# 플로이드 와샬
for v in range(n):
for a in range(n):
for b in range(n):
if a != b:
roads[a][b] = min(roads[a][b],roads[a][v]+roads[v][b])
# 가장 긴 시간이 걸리는 마을
max_time = 0
for i in range(n):
if i != x:
max_time = max(max_time,roads[i][x]+roads[x][i])
# 출력
print(max_time)
구현이 쉬워서 한번씩 던져보기 아주 좋다. 그러나 O(V^3)의 시간복잡도로는 이 문제는 풀 수 없었다.
그 다음으로 생각은 자연스럽게 다익스트라 알고리즘으로 넘어간다. 일단 각 마을 i 에서 다익스트라를 사용해서 x 까지의 최단거리를 구하고, x에서는 한번만 다익스트라를 수행해서 답을 구하는 방식이다. 이렇게 되면 다익스트라를 n + 1 번 수행하게 되니 시간 복잡도는 O(V^2 * logV) 가 될 것이다.
내 코드(다익스트라):
# dawitblog.tistory.com/169
import sys
from heapq import heappop,heappush
input = sys.stdin.readline
INF = sys.maxsize
# 입력
n,m,x = map(int,input().split())
x -= 1
# 길 소요시간 리스트
roads = [[] for _ in range(n)]
for _ in range(m):
a,b,t = map(int,input().split())
a -= 1
b -= 1
roads[a].append((b,t))
# 다익스트라
def dijkstra(start, distance):
hq = []
heappush(hq,(0,start))
distance[start] = 0
while hq:
dist , now = heappop(hq)
if distance[now] < dist:
continue
for new in roads[now]:
cost = dist + new[1]
if cost < distance[new[0]]:
distance[new[0]] = cost
heappush(hq,(cost,new[0]))
return distance
# x부터 다른 마을로 가는 최단거리
x_distance = dijkstra(x,[INF]*n)
max_time = 0
for i in range(n):
if i != x:
max_time = max(max_time,dijkstra(i,[INF]*n)[x] + x_distance[i])
# 출력
print(max_time)
해당 코드로 통과는 했지만 시간이 1288ms 로 썩 좋지 않았다. 그래서 어떻게 개선을 할 수 있을까 생각해봤는데, 아주 획기적으로 다익스트라 단 2번만에 답을 구할 수 있었다. 처음부터 역방향 그래프를 만들어놓고 x를 시작점으로 하여서 다익스트라를 수행하면, 거꾸로 그 결과는 원래의 그래프에서 각 마을에서 x로 가는 최단거리를 모두 구한 것이 된다.
내 코드(다익스트라):
# dawitblog.tistory.com/169
import sys
from heapq import heappop,heappush
input = sys.stdin.readline
INF = sys.maxsize
# 입력
n,m,x = map(int,input().split())
x -= 1
# 길 소요시간 리스트
roads = [[] for _ in range(n)]
# 역방향 리스트
rev_roads = [[] for _ in range(n)]
for _ in range(m):
a,b,t = map(int,input().split())
a -= 1
b -= 1
roads[a].append((b,t))
rev_roads[b].append((a,t))
# 다익스트라
def dijkstra(graph , start, distance):
hq = []
heappush(hq,(0,start))
distance[start] = 0
while hq:
dist , now = heappop(hq)
if distance[now] < dist:
continue
for new in graph[now]:
cost = dist + new[1]
if cost < distance[new[0]]:
distance[new[0]] = cost
heappush(hq,(cost,new[0]))
return distance
# x부터 다른 마을로 가는 최단거리
x_other = dijkstra(roads,x,[INF]*n)
# 각 마을에서 x로 가는 최단거리(역방향 그래프 이용)
other_x = dijkstra(rev_roads,x,[INF]*n)
# 출력
print(max([x_other[i] + other_x[i] for i in range(n) if i != x]))
최종적으로 시간 복잡도는 다익스트라 2번으로 O(V * logV) 이다. 시간도 84ms로 유의미하게 줄었다.
'PS > solved.ac' 카테고리의 다른 글
| [CLASS 4]백준 1167번 - 트리의 지름 (0) | 2021.06.30 |
|---|---|
| [CLASS 4]백준 14938번 - 서강그라운드 (0) | 2021.06.29 |
| [CLASS 4]백준 11404번 - 플로이드 (0) | 2021.06.28 |
| [CLASS 4]백준 10830번 - 행렬 제곱 (0) | 2021.06.03 |
| [CLASS 4]백준 9935번 - 문자열 폭발 (0) | 2021.05.31 |




댓글